Pochi giorni fa, un collega del mio stesso team che vive a San Francisco, ha deciso di terminare la sua avventura con la nostra compagnia per provare una nuova esperienza.
L'ho sempre reputato una bravissima persona sebbene, a mio modestissimo parere, non eccelso tecnicamente.
Quando sono venuto a conoscienza del suo nuovo posto di lavoro, una delle big company presenti in Silicon Valley, mi sono posto un po' di quesiti.
Noi, come persone, ci sottovalutiamo? Ci sopravvalutiamo? Pensiamo di essere dei buoni a nulla? Abbiamo l'impressione che gli altri siano sempre più bravi di noi?
Maghi VS Dati 🧙♂️ 🔮 🆚 👩🏫 📊
Anzichè andare da qualche stregone per cercare delle risposte, ho deciso di tentare un approccio più scientifico, strada ben più sicura da intraprendere, la cui scelta dovrebbe rappresentare la normalità (purtroppo non è sempre così).
Prima riflessione, partiamo con un postulato triste ma, ahimè, vero: tu che stai leggendo queste righe, non sei il miglior ingegnere / sviluppatore / developer al mondo (la logica si può applicare a quasi tutti i mestieri). Nemmeno chi ha scritto questo articolo lo è... siamo in due. ✌️😅
Altro fatto: tu che leggi, sicuramente, non sei il peggior ingegnere / sviluppatore / developer del mondo (spero di non esserlo nemmeno io 😆 ).
💡 Siamo nella media, quasi tutti lo sono.
➡️ Sai perché? Si chiama statistica.
Assumiamo che le abilità ingegneristiche seguano una distribuzione normale, partendo dal peggiore del mondo fino ad arrivare al super genio, in questo modo:
Che cosa è una distribuzione normale?
Fra le densità di probabilità continue, la più importante è la densità di probabilità normale, detta anche distribuzione di Gauss, in onore al matematico Carl Friedrich Gauss (1777-1855).
Essa è anche nota come legge degli errori, perché descrive la distribuzione degli errori casuali relativi a successive misure di una quantità fisica; inoltre diversi fenomeni continui seguono approssimativamente una distribuzione normale.
Definiamo formalmente la differenza tra un bravo ed un cattivo ingegnere: quest'ultimo ha maggiore probabilità di non essere assunto dopo aver sostenuto un colloquio oppure di non mantenere il proprio posto di lavoro a lungo.
Questo tipo di distribuzione ha la forma di una curva gaussiana come quella in figura. 👇🏿
L'ingegnere medio è quello nel punto medio: la linea rossa sottilissima che si trova al centro della curva corrispondente al punto più alto.
Probabilmente una persona del genere non esiste, proprio come non esiste una famiglia italiana media, la cui composizione è fatta di 2,4 persone (fonte ISTAT) dato che è impossibile vederne passeggiare una al centro commerciale, composta da due persone ed una quasi mezza persona. 😝
Ora, per ottenere le conclusioni che andremo ad illustrare a breve, abbiamo bisogno di standardizzare la nostra distribuzione normale.
Niente paura, non mostreremo nessun calcolo ma è bene precisare che la standardizzazione è un procedimento che riconduce una variabile aleatoria distribuita secondo una media μ e varianza σ2, ad una variabile aleatoria con distribuzione standard, ossia di media μ con valore zero e varianza σ2 uguale a 1.
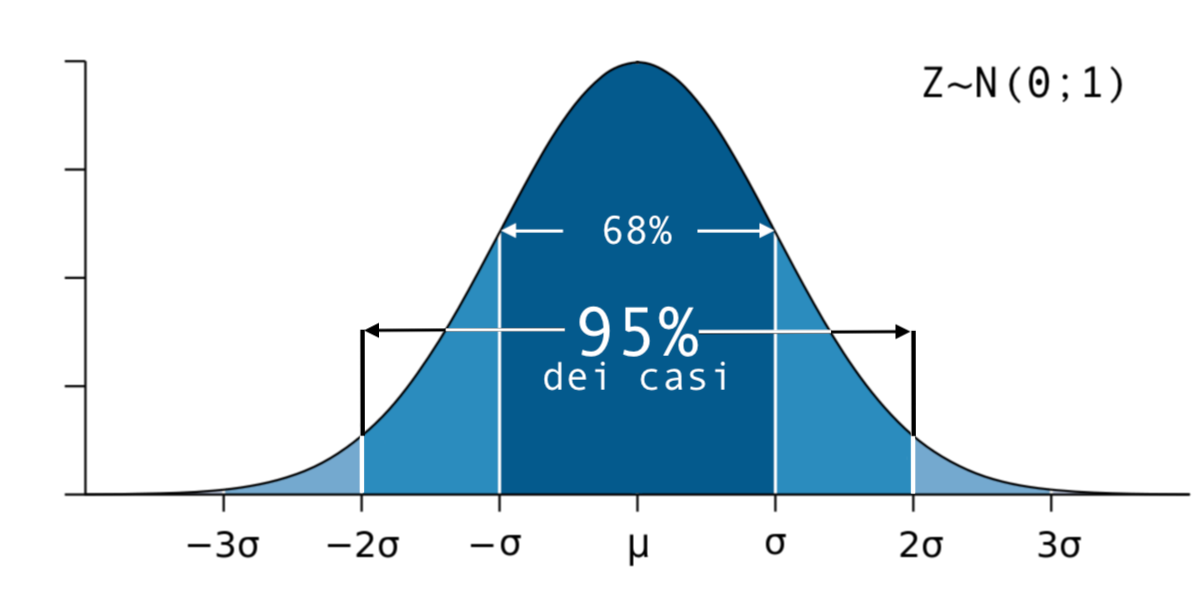
Si denota con Z~N(0;1) perchè la nostra distribuzione standardizzata Z segue la precedente distribuzione normale N con media uguale a 0 e varianza uguale a 1.
Possiamo sempre standardizzare una distribuzione normale quindi non stiamo facendo nulla che la matematica vieti (nota bene: tutto questo processo si può effettuare / dimostrare con numeri e calcoli veri, non sono stati inseriti altrimenti solamente pochi avrebbero continuato la lettura).
Eccola la standardizzata in tutto il suo splendore: 👇
Adesso che la nostra distribuzione è standard, riusciamo finalmente a capire ciò che si intende quando si parla di "valori secondo la media": sono quei valori presi nell'intervallo più vicino al valore medio, che va da μ - σ a μ + σ (ricordiamo che μ sta per media e σ indica lo scarto quadratico medio o deviazione standard).
Utilizzando le tavole statistiche, possiamo scoprire che nell’intervallo che va da μ − σ a μ + σ cadono circa il 68% dei casi, sempre.
Cosa significa? Che il 68% degli ingegneri è nella media. La maggior parte degli ingegneri è nella media. Presi 100 ingegneri, 68 di loro cadono in quel range, con valori di bravura che si avvicinano più o meno alla bravura del nostro ipotetico ingegnere medio:
Pertanto, è molto probabile che anche tu ed io siamo nella media.
Pensate che l'80% delle persone a cui è stata chiesta un'opinione sulla propria abilità di guida, ha affermato di essere migliore della media!
Sì: l'80% dei conducenti pensa di essere sopra la media (fonte della ricerca).
Di sicuro non hanno letto questo post prima di rispondere.
Se consideriamo l'intervallo successivo della nostra distribuzione standard, quello che va da μ − 2σ a μ + 2σ, avremo addirittura il 95% della popolazione: letteralmente quasi tutti, tranne una piccola parte di popolazione che rappresenta le eccezioni.
Quello che stiamo affermando è essenzialmente quale sia la probabilità che, prendendo a caso un ingegnere nel mondo, questo abbia un determinato valore di bravura.
Più specificatamente, la probabilità che un individuo scelto a caso sia bravo circa quanto il nostro ipotetico ingegnere medio è del 68%, se aggiungiamo quelli un po' più bravi o un po' meno bravi, è del 95% e a sua volta, se comprendiamo quelli decisamente più bravi o molto più scarsi, del 99%.
Avrete capito quindi la regola: i vari esempi riportati non sono altro che μ ± σ, μ ± 2σ e μ ± 3σ.
Questi sono solo alcuni dei valori, ci sono delle tabelle per qualsiasi deviazione dal valore medio.
Il ± è dovuto al fatto che la distribuzione è simmetrica attorno al suo valore medio.
Volendo essere più precisi e formali, possiamo dire che campionando a caso in una popolazione normalmente distribuita ho una probabilità pari al 68,27% di ottenere un valore compreso fra μ − σ e μ + σ : più di metà dell’intera popolazione non si allontana dal valore medio μ per più di σ.
In modo analogo, se calcoliamo l’area fra μ − 2σ e μ + 2σ otteniamo il valore 0.9544, pari al 95,44% dell’area
totale.
Questo significa che più del 95% degli elementi di una popolazione normalmente distribuita non si allontanano dal suo valore medio μ per più di 2σ.
Infine, calcolando l’area fra μ − 3σ e μ + 3σ otteniamo il 99.73% dell’area totale: la quasi totalità di una popolazione normalmente distribuita non si allontana dalla propria media per più di 3 deviazioni standard.
Perché abbiamo voluto fare questo ragionamento?
Perché molto frequentemente, anche se non abbiamo questa impressione, la nostra bravura è comparabile a quella di tutti gli altri ed è un fatto importante da tenere a mente.
La sindrome dell'impostore 👮
Wikipedia dice che la sindrome dell'impostore (dall'inglese impostor syndrome, o anche impostor phenomenon) è un termine coniato nel 1978 dalle psicologhe Pauline Clance e Suzanne Imes per descrivere una condizione psicologica particolarmente diffusa fra le persone, caratterizzata dall'incapacità di interiorizzare i propri successi e dal terrore persistente di essere esposti in quanto "impostori".
A dispetto delle dimostrazioni esteriori delle proprie competenze, le persone affette da tale sindrome rimangono convinte di non meritare il successo ottenuto. Esso viene tipicamente ricondotto a fattori quali la fortuna o il tempismo, oppure ritenuto frutto di inganno o della sopravvalutazione da parte di coloro che hanno avuto il compito di giudicarli.
A me capita, ad esempio quando qualcuno mi dice che l'articolo che ho scritto gli è piaciuto, oppure quando i miei colleghi sostengono io abbia fatto un buon lavoro.
Tutti hanno la sindrome dell'impostore, è normale e si manifesta di più quando si è circondati da gente che ne sa molto più di te.
Però, c'è anche qualcos'altro che si ottiene quando si è circondati da questo tipo di persone: crescita. 💥
Spesso si evitano delle opportunità perché non si è sicuri di esserne all'altezza, invece non è così.
Si può afferrare il toro dalle corna e fronteggiarlo: il più grande potere che abbiamo è capirci qualcosa e gestire la situazione, qualsiasi essa sia.
Si prende un problema che non si è mai risolto prima e lo si risolve.
Questo è ciò che fanno gli ingegneri.
La sindrome da impostore? Facciamocela amica: quel fastidioso conoscente che ti ricorda che stai per fare qualcosa di troppo difficile, di cui non conosci nulla, mentre sei circondato da esperti che potrebbero farlo col minimo sforzo, non sa che se sei circondato da tali individui, significa che hai qualcuno a cui chiedere grazie ai quali andrà tutto bene.
Il fatto di avere più conoscenza su un determinato argomento non significa che queste persone posseggano più competenza su tutto.
Quindi, cosa fai quando pensi di non essere abbastanza bravo?
- Ammettere di sentirsi in questo modo.
- Pensare al motivo per cui si ha questa sensazione.
- Iniziare a fare cose.
Non si sa come fare qualcosa? Si impara.
Il team in cui si lavora è meglio di noi? Bene! Si fanno domande e si usa la squadra come una risorsa.
Siamo bloccati e non si riesce a combinare nulla?
Una pausa aiuta di sicuro, dopodichè si prova con un approccio diverso (i crediti per questa perla vanno al mio collega Davide M. 🤩 ).
Ansia?
Teniamo traccia dei successi: ogni qual volta si completa un progetto difficile, si annota scrivendo due righe su un file riguardo cosa lo ha reso difficile, come lo si è risolto e quali ostacoli si sono superati.
La prossima volta che ci si trova in difficoltà, si apre il file e si legge. 🤓
Aggiungiamone sempre di nuovi.
Ci si ricordi di quanto fatto quando la motivazione è bassa ed i tempi sono difficili, senza sedersi sugli allori!
Quali sono i 5 risultati di cui sei più orgoglioso? Scrivimelo via mail.
PS: Male che va, si può sempre riciclare questa lista per ricordare al tuo capo perché dovrebbe darti un aumento 🤑